hävbar diskontinuitet
Substantiv
hävbar diskontinuitet
- (matematik) diskontinuitet av funktion
 i punkt
i punkt  där både vänster- och högergränsvärde existerar (ändligt) och är lika med värdet
där både vänster- och högergränsvärde existerar (ändligt) och är lika med värdet  , varför funktionen kan göras kontinuerlig i punkten genom att definiera
, varför funktionen kan göras kontinuerlig i punkten genom att definiera 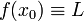
- Funktionen
 har en hävbar diskontinuitet i
har en hävbar diskontinuitet i  , ty såväl höger- som vänstergränsvärde existerar ändligt och är lika med 1.
, ty såväl höger- som vänstergränsvärde existerar ändligt och är lika med 1.
- Funktionen
Översättningar
Översättningar
- engelska: removable discontinuity
 i punkt
i punkt  där både vänster- och högergränsvärde existerar (ändligt) och är lika med värdet
där både vänster- och högergränsvärde existerar (ändligt) och är lika med värdet  , varför funktionen kan göras kontinuerlig i punkten genom att definiera
, varför funktionen kan göras kontinuerlig i punkten genom att definiera 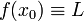
 har en hävbar diskontinuitet i
har en hävbar diskontinuitet i  , ty såväl höger- som vänstergränsvärde existerar ändligt och är lika med 1.
, ty såväl höger- som vänstergränsvärde existerar ändligt och är lika med 1.