maximipunkt
Substantiv
maximipunkt
- (matematik, till en reellvärd funktion f av en reell variabel) punkt
 sådan att det existerar ett
sådan att det existerar ett  sådant att
sådant att  för varje
för varje ![x \in ]x_0 - \epsilon, x_0 + \epsilon[](//upload.wikimedia.org/math/0/b/a/0ba02cfbd7b6edc55ad22fe5c36267fa.png) ; om sträng olikhet råder säges punkten vara en sträng maximipunkt
; om sträng olikhet råder säges punkten vara en sträng maximipunkt
- Punkten
 är en sträng lokal maximipunkt för funktionen
är en sträng lokal maximipunkt för funktionen  .
. - Hyperonymer: extrempunkt
- Punkten
- (matematik, till en reellvärd funktion f av flera reella variabler) punkt
 sådan att det existerar ett öppet klot
sådan att det existerar ett öppet klot  kring
kring  sådant att
sådant att 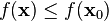 för varje
för varje  ; om sträng olikhet råder säges punkten vara en sträng maximipunkt
; om sträng olikhet råder säges punkten vara en sträng maximipunkt
- Punkten
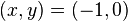 är en sträng lokal maximipunkt för funktionen
är en sträng lokal maximipunkt för funktionen 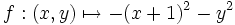 .
. - Hyperonymer: extrempunkt
- Punkten
- Användning: De matematiska termerna beskrivna ovan kallas mer precist för lokal maximipunkt, och bör inte blandas ihop med begreppet global maximipunkt vilket är en punkt
 sådan att
sådan att  .
.
 sådan att det existerar ett
sådan att det existerar ett  sådant att
sådant att  för varje
för varje ![x \in ]x_0 - \epsilon, x_0 + \epsilon[](http://upload.wikimedia.org/math/0/b/a/0ba02cfbd7b6edc55ad22fe5c36267fa.png) ; om sträng olikhet råder säges punkten vara en sträng maximipunkt
; om sträng olikhet råder säges punkten vara en sträng maximipunkt
 är en sträng lokal maximipunkt för funktionen
är en sträng lokal maximipunkt för funktionen  .
. sådan att det existerar ett
sådan att det existerar ett  kring
kring 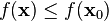 för varje
för varje  ; om sträng olikhet råder säges punkten vara en sträng maximipunkt
; om sträng olikhet råder säges punkten vara en sträng maximipunkt
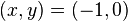 är en sträng lokal maximipunkt för funktionen
är en sträng lokal maximipunkt för funktionen 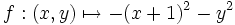 .
. sådan att
sådan att  .
.